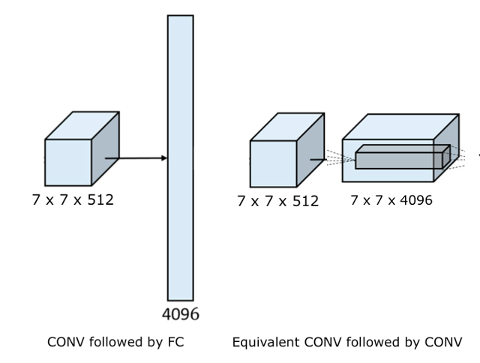
Conversion Fully Connected Layer to Convolutional layer
For any CONV layer there is an FC layer that implements the same forward function. The weight matrix would be a large matrix that is mostly zero except for at certain blocks (due to local connectivity) where the weights in many of the blocks are equal (due to parameter sharing) Source: cs231n.
If we take a look at VGG16 neural architecture we can see that the output
dimension of the last convolutional layer is $7 \times 7 \times 512$.
The next leayer is FC layer and has dimension $1\times1\times4096$.
To get the same dimension of the output using convolutions we just need to create $4096$ filters of size $7\times7$.
FCN for Semantic segmentation
Given neural network trained on classification task. The main idea is to substitute the last fully connected layer by convolution layer. If we then scale up this last layer to our input image size we get a segmentation mask. These direct prediction of FCN are typically in low resolution, because the resolution of output feature maps is downsampled.
Upsampling is done by transposed convolution (or deconvolution).
This is because, deep features can be obtained when going deeper, spatial location information is also lost when going deeper.
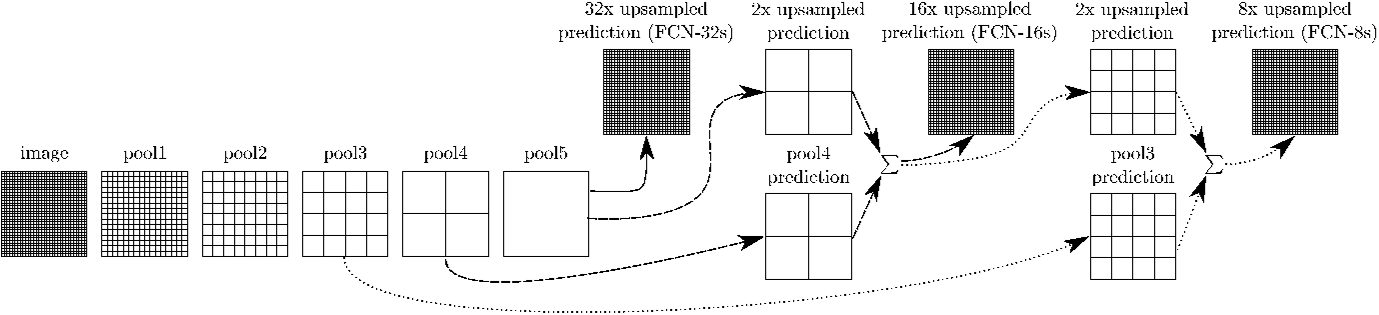
FCN-32, FCN-16, FCN-8
(Some notes on the report Fully Convolutional Networks for Semantic Segmentation)
Main features:
- As the base network VGG16 is used
- Upsampling via deconvolution
- Fusing the output (skip connections)
FCN-32:
- the last fully connected layer (layer_7) is replaced by a $1\times1$ convolution layer conv_7 (see conversion)
- Directly produces the segmentation map from conv7, by using a transposed convolution layer with stride 32.
FCN-16:
- the last fully connected layer (layer_7) is replaced by a $1\times1$ convolution layer conv_7 (see conversion)
- new layer (conv_7) is upsampled 2 times to match dimensions with pool_4 using transposed convolution with $(kernel=4, stride=2, padding=same)$. The skip connection between pool_4 and conv_7 is added
- conv_8 is upsampled 8 times to match dimensions with input image size using transposed convolution with $(kernel=32, stride=16, padding=same)$. At the end we get the number of channels equal to the number of classes
FCN-8:
- the last fully connected layer (layer_7) is replaced by a $1\times1$ convolution layer conv_7 (see conversion)
- new layer (conv_7) is upsampled 2 times to match dimensions with pool_4 using transposed convolution with $(kernel=4, stride=2, padding=same)$. The skip connection between pool_4 and conv_7 is added
- conv_8 is upsampled twice to match dimensions with pool_3 using transposed convolution with $(kernel=4, stride=2, padding=same)$ The skip connection between layer_3 and conv_9 is added
- conv_9 is upsampled 4 times to match dimensions with input image size using transposed convolution with $(kernel=16, stride=8, padding=same)$. At the end we get the number of channels equal to the number of classes