Popular architectures
Resnet
Resnet module
With the network depth increasing accuracy gets saturated and it is not a problem of overfitting, as it might first appear. In simple words if we add some additional layers to pretraied network, new bigger network should work as good as the shallow or even better. Resnets solve this problem, namely vanishing gradient problem.
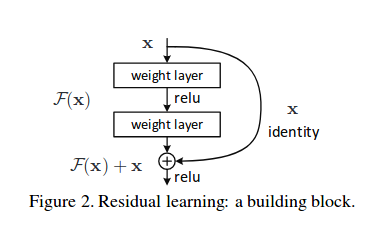
Let us focus on a local (a few layers of a network) neural network with desired mapping $H(x)$. We let this network fit another mapping $F(x) = H(x) - x$. The original mapping is recast into $F(x) + x$.
Author’s hypothesis is that it is easier to optimize this residual mapping $F(x)$ than to optimize the original unreferenced mapping $H(s)$.
Formally building block (or residual unit) performs the following computation:
\[
\begin{split}
&y_l = x_l + F(x_l, W_l) \\\
&x_{l + 1} = f(y_l)
\end{split}
\tag{1}\label{eq1}
\]
where $f$ is activation function, $W_l$ is weights matrix of the layer $l$.
We see that dimensions of $x_l$ and $F$ must be equal. If this is not the case we perform linear projection $A$ which can be trainable or simply pad 0s to $x_l$.
\[ \begin{equation} y_l = Ax_l + F(x_l, W_l) \end{equation} \]
Authors considered general form of the first equation: \[ \begin{equation} y_l = h(x_l) + F(x_l, W_l) \end{equation} \] and they showed by experiments that the identity mapping is sufficient for addressing this problem.
Analysis
Let us take as activation function $f(x) = ReLU(x)$: \[ \begin{equation} x_{l+1} = x_l + F(x_l, W_l) \end{equation} \]
\[ \begin{equation} x_{L} = x_l + \sum_{i=l}^{i=L-1}F(x_i, W_i) \end{equation} \]
Denoting loss functions as $C$, from the chain rule of backpropagation we get: \[ \begin{equation} \frac{\partial C}{\partial x_l} = \frac{\partial C}{\partial x_L} \frac{\partial x_L}{\partial x_l} = \frac{\partial C}{\partial x_L} (1 + \frac{\partial}{\partial x_l} \sum_{i=l}^{i=L-1}F(x_i, W_i) ) \end{equation} \] We see that the term of $\frac{\partial C}{\partial x_L}$ ensures that information is directly propagated back to any shallower unit $l$. And it is suggested it is unlikely that the gradient $\frac{\partial C}{\partial x_L}$ to be canceled out for minibatch, because in general term $\sum_{i=l}^{i=L-1}F(x_i, W_i)$ cannot be always $-1$ for all samples in minibatch [2].
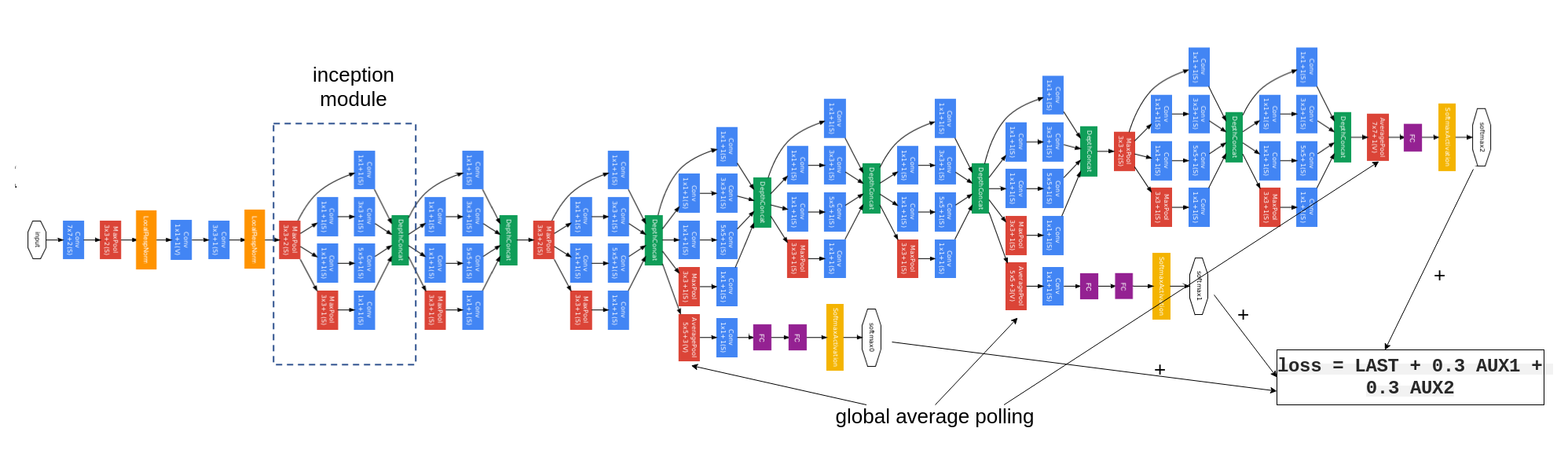
Inception
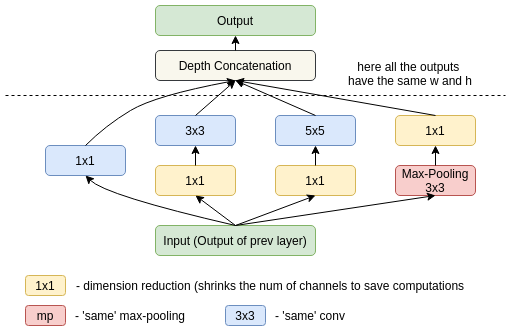
Inception v1 module
- $1\times 1$ convolutions to decrease number of channels
- $1\times 1$, $3\times 3$, $5\times 5$ filters to extract features at different scales
- average pooling layers
- auxiliary predictions and combined loss
 inception_v2_1.png
inception_v2_1.png
Inception v2 module
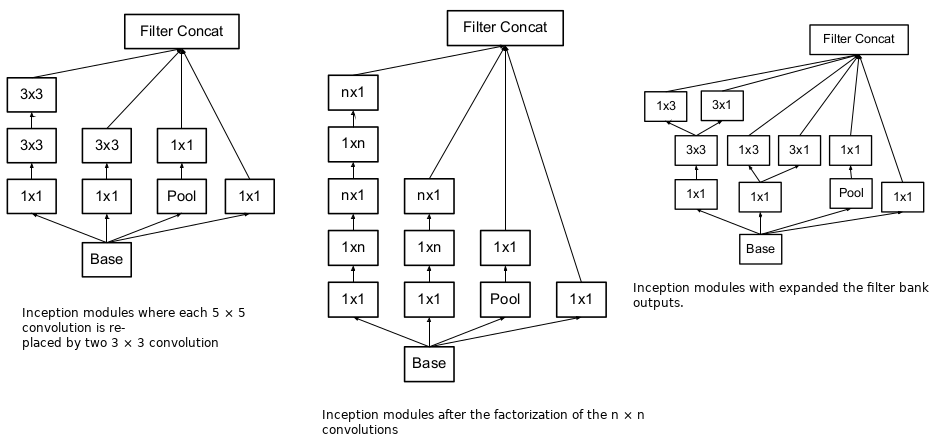
- batch normalization
- factorize 5x5 convolution to two 3x3
- $n \times n$ convolutions are decomposed into $n \times 1$ and $1 \times n$
Inception v3 module
- increased network input size $224 \times 224$ to $299 \times 299$
- convolution with stride 2 and max-polling layers are combined in one layer + depth concatenation
- only 1 auxiliary classifier is used