Problem solving approach: heap

Binary heap is based on complete binary tree. All the nodes of a max-heap (or min-heap) follow the property that the key of a node is larger than or equal (or less than or equal to) to the keys of it’s children nodes.

We represent $N$-element heap as array $pq$ of length $N+1$. The parent of the node in position $i$ is in position $\lfloor \frac{i}{2} \rfloor$. The children of the node in position $i$ are in positions $2i$ and $2i + 1$.

Note: STL PriorityQueue is implemented using max-heap

Heap order violation

If a node’s key becomes larger than parent’s key we do bottom-up reheapfy (swim).

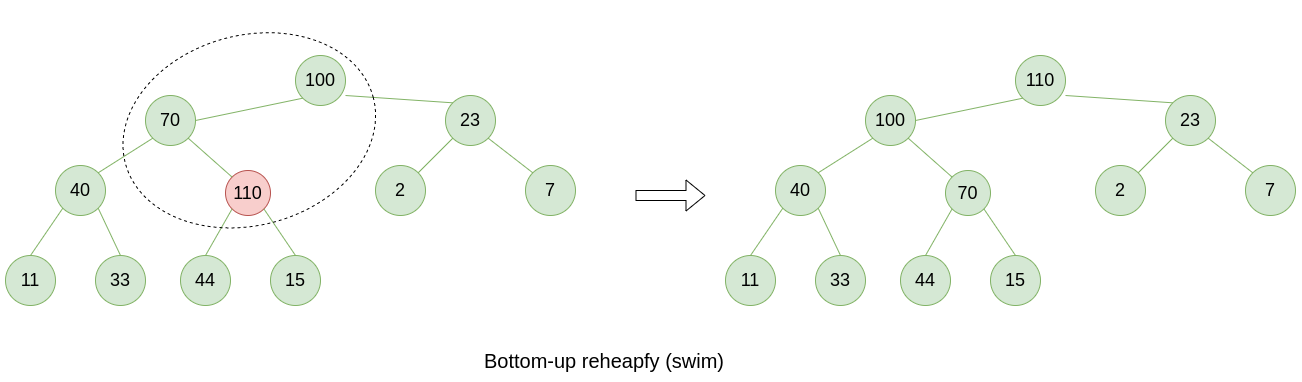
void swim(std::vector<int> &pq, int k)
{
        while (k > 1 && pq[k / 2] < pq[k])
        {
                std::swap(pq[k / 2], pq[k]);
                k /= 2;
        }
}

If a node’s key becomes smaller than child node’s key we do top-down reheapfy (sink).

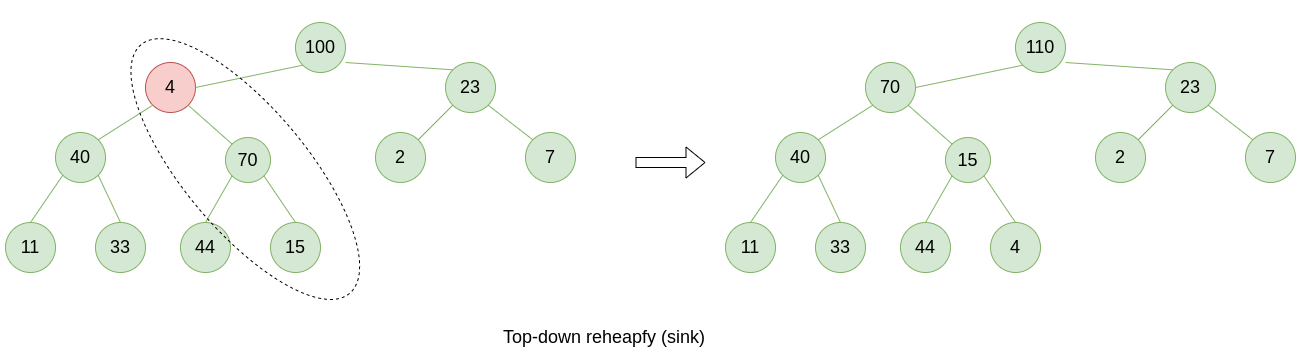
void sink(std::vector<int> &pq, int k, int n)
{
        while (2 * k  <= n)
        {
                int i = 2 * k;
                if (i < n && pq[i + 1] > pq[i])
                        i++;
                if (pq[i] < pq[k])
                        break;
                std::swap(pq[i], pq[k]);
                k = i;
        }
}

Both of them are $O(log(n))$.

Building a heap

void build_heap(std::vector<int> &pq, int n)
{
    for (int i = n / 2; i > 0; i--)
        sink(pq, i);
}

Complexity is $O(n)$ (fewer than $2n$ compares and fewer than $n$ exchanges).

Insertion and removing the maximum (minimum)

Insertion. To insert new element to the heap we add new element at the end of array, increment the heap size and then swim up with that key.

void insert(std::vector<int> &pq, int el, int n)
{
    assert(pq.size() > n);
    pq[++n] = el;
    swim(pq, ) for (int i = n / 2; i > 0; i--)
        sink(pq, n);
}

Removing the maximum (minimum). We take the largest key off the top, put the item from the end at the top, decrement heap size and then sink down with the element.

int delete_max(std::vector<int> &pq, int n)
{
    int ret = pq[1];
    std::swap(pq[1], pq[n--]);
    sink(pq, 1, n)
}

Both of them are $O(log(n))$.

Heapsort

int heapsort(std::vector<int> &pq) // size = n + 1
{
    int n = pq.size();
    build_heap(pq, n);

    while (n > 1)
    {
        swap(pq[1], pq[n--]);
        sink(pq, 1, n);
    }
}

Complexity is $O(n log(n))$. Heapsort has poor cache performance.